Das ccc Axiom, das zum Zermelo Fraenkel Sytem noch ein unabhängiges Axion hinzufügt ist mit Sicherheit ein wichtiges Axiom. Es geht darum, dass jede Familie paarweise disjunkter offener Mengen wiederum eine abzählbare Überdeckung besitzt. Welche Implikationen daraufhin aus der Kategorientheorie für die Kombinatoren zu folgern sind ? Schließlich ist die Theorie der Topen und damit der Aussagenlogik und Mengenlehre darin konstruierbar. Jedenfalls sieht man hier Gödels Vermutung impliziet dann wieder bestätigt , falls man das in die Konstruktion der jeweiligen Kategorien mit einbezieht..
... link
Als 52 Jähriger ist man für das Marketing schon Senior (siehe dazu die Webpage)
https://www.thyssenkrupp-homesolutions.de/ratgeber/magazin/aktiv-leben/ab-wann-gelten-wir-als-alt/#:~:text=Der%20Ausdruck%20Senior%20ist%20nichts,Personen%20in%20verschiedenen%20Bereichen%20erm%C3%B6glicht.&text=Aus%20diesem%20Grund%20k%C3%B6nnen%20wir,Umfeld%20als%20Senior%20definiert%20werden.Warum man als Senior in dieser Gesellschaft immer noch benachteiligt ist. Schließlich gehöre ich zu einer Minderheit (den Marketing- Senioren) die ein nachwachsender Rohstoff durch alle Schichten der Gesellschaft hindurch ist.
... link
Es stimmt , die Topologie des Niemietzky -Raums ist nicht normal. Für die beiden Mengen der einen begrenzenden Zahlengeraden kann man Q (die rationalen Zahlen) und I (die Irrationalen Zahlen) als Beispiel nehmen. Beide Mengen sind in der Niemietzky-Topologie abgeschlossen, dennoch existieren, dank der speziellen Definition der Umgebungsbasis, für die beiden Punktmengen keine zwei offenen Umgebungen U und V von Q und I die disjunkt sind.
Interessanter sind dann die Beispiele , in denen die Homotopie-Gruppe mindestens so mächtig wie die ganzen Zahlen sind und gleichzeitig ein Rand mit Niemietzky-artiger - Topologie definiert wird. ( Wie voher über den berührenden Kreis am Rand etc.) Da macht man nämlich um den Rand einen Bogen.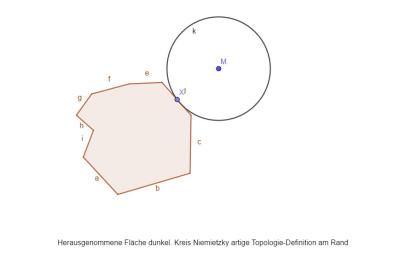
Eigentlich müßte der Rand unendlich oft differenzierbar sein um eine Niemietzky-artige Definition der Topologie-Basis zu konstruieren. Man kann aber bei fünf Wurscht-Punkten vielleicht noch eine andere Topologie unterstellen. Fakt bleibt dass der Rand trotzdem nicht normal ist und bis auf die 0-homotopen Kurven alles um den extremen Rand einen Bogen macht .
... link