Es stimmt , die Topologie des Niemietzky -Raums ist nicht normal. Für die beiden Mengen der einen begrenzenden Zahlengeraden kann man Q (die rationalen Zahlen) und I (die Irrationalen Zahlen) als Beispiel nehmen. Beide Mengen sind in der Niemietzky-Topologie abgeschlossen, dennoch existieren, dank der speziellen Definition der Umgebungsbasis, für die beiden Punktmengen keine zwei offenen Umgebungen U und V von Q und I die disjunkt sind.
Interessanter sind dann die Beispiele , in denen die Homotopie-Gruppe mindestens so mächtig wie die ganzen Zahlen sind und gleichzeitig ein Rand mit Niemietzky-artiger - Topologie definiert wird. ( Wie voher über den berührenden Kreis am Rand etc.) Da macht man nämlich um den Rand einen Bogen.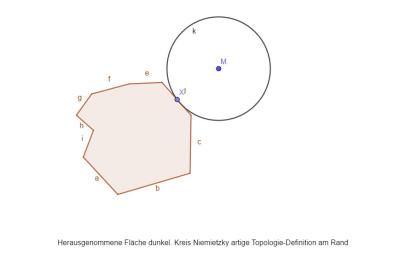
Eigentlich müßte der Rand unendlich oft differenzierbar sein um eine Niemietzky-artige Definition der Topologie-Basis zu konstruieren. Man kann aber bei fünf Wurscht-Punkten vielleicht noch eine andere Topologie unterstellen. Fakt bleibt dass der Rand trotzdem nicht normal ist und bis auf die 0-homotopen Kurven alles um den extremen Rand einen Bogen macht .
... link