Geroch für die Schwarzschild-Metriken
Man könnte es kaum glauben es gibt Geroch für die Schwarzschild-Metriken und das obwohl die Niemietzky -Topologie nicht normal ist .
Das Theorem von Geroch lautet :
Sei M eine zeitorientierte kausal kompakte Raumzeit , die zwischen einer Anfangsfläche S_1 und S_2 interpoliert. M enthalte keine geschlossenen zeitartigen Kurven. Dann ist S_1 diffeomorph zu S_2 und M diffeomorph zu S_1x[0,1]
Dass man da nicht genug von Geroch hat, wo das was mit der Schwarzschild-Lösung zu tun hat, da kann man ja jenseits des Erwartungshorizonts mit hineinfallen .
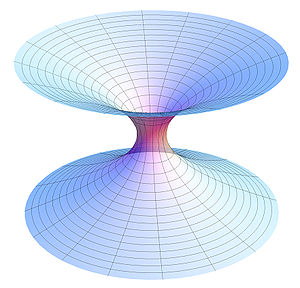
Oder, obwohl man das dann nicht glaubt ,zum Wurmloch werden.
Mehr dazu in der wikipedia
https://en.wikipedia.org/wiki/Geroch%27s_splitting_theoremVielleicht hat das ja was mit dem Satz von Sard zu tun
Bei dem die kritischen Werte einer Abbildung zwischen 2 Mannigfalitigkeiten lebesgue Nullmengen sein müssen.
Falls gibt es vielleicht irgend wann den Satz von Sard, Geroch über Wurmlöcher , das wär doch mal was oder ? Der geht dann bestimmt in die Annalen ein.
Für den Satz von Sard siehe :
https://de.wikipedia.org/wiki/Satz_von_Sard#:~:text=Der%20Satz%20von%20Sard%2C%20auch,Abbildungen%20in%20der%20Singularit%C3%A4tentheorie%20bzw.